LSST will measure the shapes of billions of galaxies to increase our understanding of dark energy by mapping distortions in shapes due to cosmic shear. With this unprecedented statistical precision, a deep understanding of potential systematic biases will be required. In this LSST DESC repository, we investigate biases originating from two chromatic effects in the atmosphere: (i) differential chromatic refraction (DCR) and (ii) wavelength dependence of seeing. These biases arise when using the point spread function (PSF) measured with stars to estimate the shapes of galaxies with different spectral energy distributions (SEDs) than the stars.
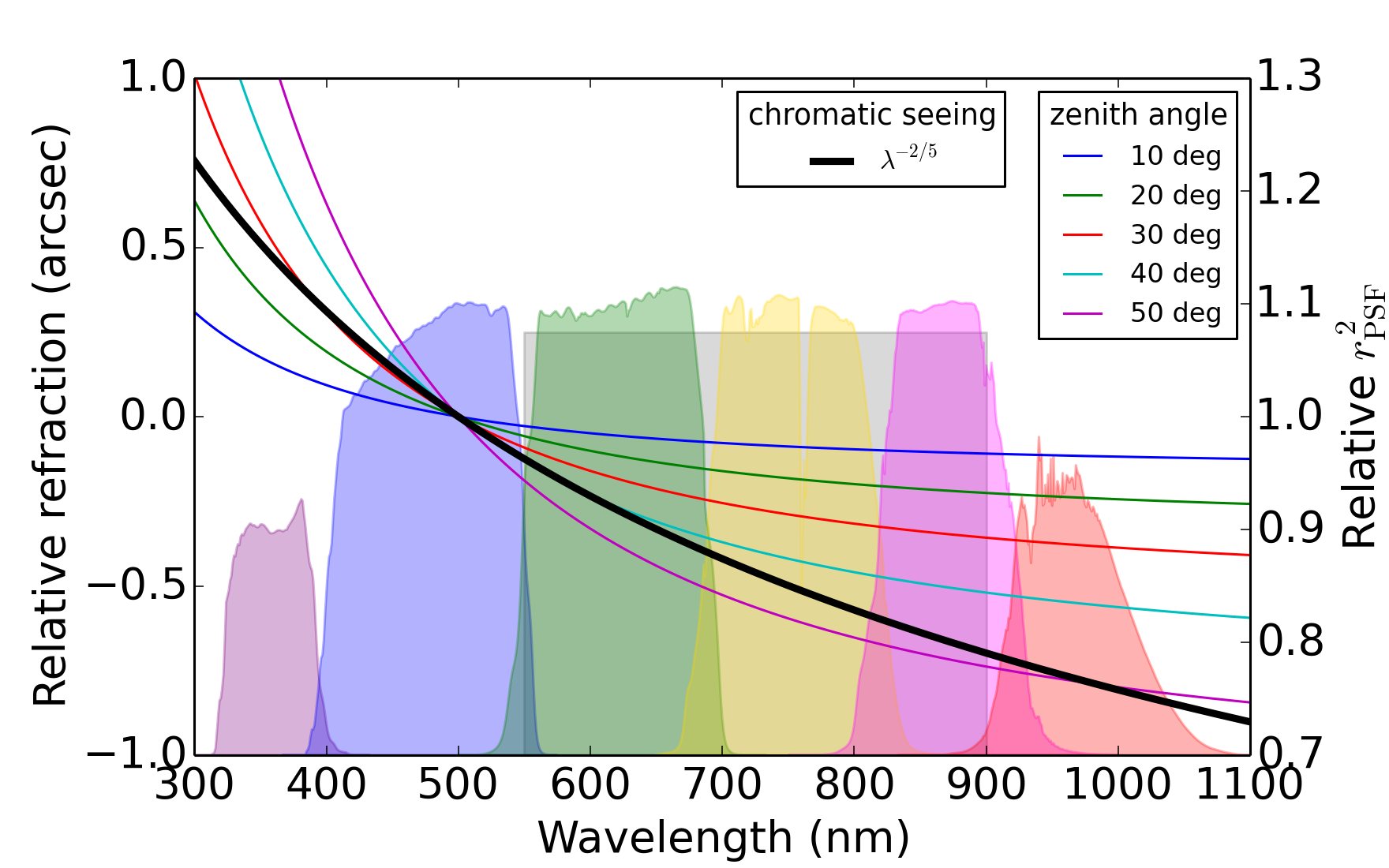
DCR is the effect that bluer photons are bent slightly more toward the zenith when entering the atmosphere than are redder photons (Figure 1). For example, at a zenith angle of 35 degrees, which will be approximately the median for LSST, a photon at the blue end of the \(r\) filter will land about 0.15 arcseconds closer to the zenith than a photon at the red end of the \(r\) filter, or about 25% of the PSF FWHM. This leads to both an SED-dependent shift in PSF centroid and SED-dependent stretching of the PSF in the zenith direction. These effects can be quantified in terms of the shifts in the PSF zenith-direction first and second moments, denoted \(\bar{R}\) and \(V\), respectively.
Atmospheric turbulence smears out blue photons somewhat more than red photons, in the sense that the relationship between FWHM and wavelength goes like \(\mathrm{FWHM} \propto \lambda^{-1/5}\). This effect can be characterized as an SED-dependent shift in the second moment square radius \(r^2\), which is equal to the sum of the two second moments measured in perpendicular directions, and scales like \(\lambda^{-2/5}\) (see Figure 1). As a consequence, the PSF at the blue end of the \(r\) filter is about 4.5% wider, or 9% larger in area, than the PSF at the red end of the \(r\) filter.
These misestimations of the PSF moments lead to systematic errors in galaxy shape measurement. It is common to characterize such biases in terms of the additive and multiplicative shear calibration parameters \(m\) and \(c\), defined by \[\hat{\gamma_i} = (1+m_i)\gamma_i + c_i.\] where \(\hat{\gamma_i}\) is the shear estimator and the true shear is \(\gamma_i\). With the "1" direction oriented towards the zenith, the bias from differential chromatic refraction can be written \[m_1^\mathrm{DCR} = m_2^\mathrm{DCR} = \frac{- \Delta V}{r^2_\mathrm{gal}} \] \[c_1^\mathrm{DCR} = \frac{- \Delta V}{2r^2_\mathrm{gal}} \] \[c_2^\mathrm{DCR} = 0.\] where \(\Delta V = V_\mathrm{PSF, star} - V_\mathrm{PSF, gal}\), and \(r^2_\mathrm{gal}\) is the second moment squared radius of the galaxy under consideration. Similarly, the bias for chromatic seeing becomes \[m_1^\mathrm{seeing} = m_2^\mathrm{seeing} = \frac{-r^2_{PSF}}{r^2_\mathrm{gal}}\frac{\Delta r^2_\mathrm{PSF}}{r^2_\mathrm{PSF}}\] \[c_i^\mathrm{seeing} = -\epsilon_i^\mathrm{PSF}\frac{r^2_\mathrm{PSF}}{r^2_\mathrm{gal}}\frac{\Delta r^2_\mathrm{PSF}}{r^2_\mathrm{PSF}}.\] where \(\Delta r^2_\mathrm{PSF} = r^2_\mathrm{PSF, star} - r^2_\mathrm{PSF, gal}\) and \(\epsilon_i^\mathrm{PSF}\) is the (usually small) ellipticity of the PSF. For LSST, the requirements are approximately to keep \(|m|\) and \(|c|\) below 0.003 and 0.0015, respectively.
In this repository we aim to quantify the chromatic biases expected for LSST and to investigate strategies to mitigate these biases. Our analysis consists of three parts:
In addition to its relevance to LSST, these analyses are applicable to other large-volume ground-based surveys such as DES, Hyper Suprime-Cam and KIDS, where the same atmospheric biases will manifest. The wavelength dependence of seeing present for atmospheric turbulence is also qualitatively similar to the wavelength dependence of the diffraction limit, which will affect space-based cosmic shear surveys such as Euclid.