Fitted Parameter Accuracy¶
This notebook examins the accuraccy of fitted SN parameters when assuming different levels of atmospheric variabitily in the fitting process.
[1]:
from pathlib import Path
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from astropy import units as u
from astropy.coordinates import SkyCoord
from scipy.stats.stats import pearsonr
Parsing Data¶
Results from the analysis pipeline are written to disk over multiple files. We read data from each file and concatenate the results.
Values that are not fit for are masked using the value -99.99. For conveniance, we replace these values with nan in the below example.
For a full overview of the output file data model, see the data model documentation.
[2]:
def add_derived_values(pipeline_data):
"""Calculate some useful values and add them to a dataframe of pipeline data
Args:
pipeline_data (DataFrame): Pipeline data returned by ``load_pipeline_data``
Returns:
A copy of the given dataframe with added columns
"""
pipeline_data = pipeline_data.copy()
for param in ('z', 't0', 'x0', 'x1', 'c'):
pipeline_data[f'delta_{param}'] = pipeline_data[f'fit_{param}'] - pipeline_data[param]
pipeline_data[f'delta_{param}_norm'] = pipeline_data[f'delta_{param}'] / pipeline_data[f'{param}']
return pipeline_data
[3]:
def get_combined_data_table(directory, key, pattern='*.h5'):
"""Return a single data table from directory of HDF5 files
Returns concatenated tables from each of the files.
Args:
directory (Path): The directory to parse data files from
key (str): Key of the table in the HDF5 files
pattern (str): Include results from all files matching the regex pattern
Returns:
A pandas datafram with pipeline data
"""
if not (h5_files := list(directory.glob(pattern))):
raise ValueError(f'No h5 files found in {directory}')
dataframes = []
for file in h5_files:
with pd.HDFStore(file, 'r') as datastore:
dataframes.append(datastore.get(key))
return pd.concat(dataframes).set_index('snid')
def load_pipeline_data(directory, pattern='*.h5', derived=True):
"""Return the combined input and output parameters from a pipeline run
Args:
directory (Path): The directory to parse data files from
pattern (str): Include results from all files matching the regex pattern
Returns:
A pandas datafram with pipeline data
"""
sim_params = get_combined_data_table(directory, '/simulation/params', pattern=pattern)
fit_results = get_combined_data_table(directory, '/fitting/params', pattern=pattern)
fit_status = get_combined_data_table(directory, 'message', pattern=pattern)
# THe join order is important here. Left most tables are a superset of rightmost tables
pipeline_data = fit_status.join(fit_results).join(sim_params)
# Join results for failed fit results will be nan.
return_data = pipeline_data.replace(-99.99, np.nan)
if derived:
return_data = add_derived_values(return_data)
return return_data
[4]:
data_dir = Path('.').resolve().parent / 'data' / 'analysis_runs' / 'validation'
We load data from different simulation and fitting conditions. The fitting process may not be able to find a successful minimum for each lgiht-curve. We print a summary of the success rate.
[5]:
sim_4_fit_4 = load_pipeline_data(data_dir, pattern='pwv_sim_4_fit_4*')
print('Summary of simulation success for SNe:')
sim_4_fit_4.success.value_counts()
Summary of simulation success for SNe:
[5]:
True 957
False 43
Name: success, dtype: int64
[6]:
sim_epoch_fit_4 = load_pipeline_data(data_dir, pattern='pwv_sim_epoch_fit_4*')
print('Summary of simulation success for SNe:')
sim_epoch_fit_4.success.value_counts()
Summary of simulation success for SNe:
[6]:
True 957
False 43
Name: success, dtype: int64
[7]:
sim_epoch_fit_seasonal = load_pipeline_data(data_dir, pattern='pwv_sim_epoch_fit_seasonal*')
print('Summary of simulation success for SNe:')
sim_epoch_fit_seasonal.success.value_counts()
Summary of simulation success for SNe:
[7]:
True 957
False 43
Name: success, dtype: int64
[8]:
sim_epoch_fit_epoch = load_pipeline_data(data_dir, pattern='pwv_sim_epoch_fit_epoch*')
print('Summary of simulation success for SNe:')
sim_epoch_fit_epoch.success.value_counts()
Summary of simulation success for SNe:
[8]:
True 957
False 43
Name: success, dtype: int64
Accuracy of Fitted Parameters¶
We examine the distribution of fitted parameter residuals for different fitting conditions.
[9]:
def clean_data(data):
"""Drop SN with failed fits and apply quality cuts
Cuts defined here are applied to all plots in the remainder
of the notebook.
Args:
data (DataFrame): Pipeline output data
Returns:
A copy of the data that has been cleaned
"""
return data[data.success]
[10]:
def plot_parameter_distribution(
data,
params=('x0', 'x1', 'c'),
xlims=((0, 3.0e-5), (-4, 4), (-.5, .5)),
bins=(np.linspace(0, 3.0e-5, 100), 100, 100),
sharey=True,
figsize=(20, 5)
):
"""
Args:
data (DataFrame): Pipeline data to use for the plot
params (tuple): Tuple of parameter names to plot distributions for
bins (int): Number of bins to use when building histograms
figsize (tuple): Size of the generated figure
"""
data = clean_data(data)
fig, axes = plt.subplots(1, len(params), figsize=figsize, sharey=sharey)
for param, xlim, binn, axis in zip(params, xlims, bins, axes):
axis_data = data[param]
median = axis_data.median()
std = axis_data.std()
hist = axis.hist(axis_data, bins=binn, label=f'STD {std:.2f}')
axis.axvline(median, linestyle='--', color='k', label=f'Median: {median:.2f}')
axis.set_xlabel(param, fontsize=16)
axis.set_xlim(xlim)
axis.legend()
axes[0].set_ylabel('Number of SNe')
[11]:
def plot_parameter_accuracy(
data,
params=('x0', 'x1', 'c'),
bins=np.linspace(-1, 1, 200),
sharey=False,
figsize=(20, 5)
):
"""Plot histograms of the normalized difference between
simulated and fitted model parameters.
Args:
data (DataFrame): Pipeline data to use for the plot
params (tuple): Tuple of parameter names to plot distributions for
bins (Array): Bins to use when building histograms
figsize (tuple): Size of the generated figure
"""
data = clean_data(data)
fig, axes = plt.subplots(1, len(params), figsize=figsize, sharey=sharey)
for param, axis in zip(params, axes):
xmin = min(bins)
xmax = max(bins)
axis_data = data[f'delta_{param}_norm']
axis_data = axis_data[xmin <= axis_data][axis_data <= xmax]
median = axis_data.median()
mean = axis_data.mean()
std = axis_data.std()
hist = axis.hist(axis_data, bins=bins, label=f'STD {std:.2f}')
axis.axvline(median, linestyle='--', color='k', label=f'Median: {median:.2f}')
axis.set_xlabel(r'$\frac{' + param + r'_{sim} - ' + param + '_{fit}}{' + param + '_{sim}}$', fontsize=16)
axis.set_xlim(xmin, xmax)
axis.legend()
axes[0].set_ylabel('Number of SNe')
[12]:
print('Distribution of input parameters')
plot_parameter_distribution(sim_epoch_fit_4)
plt.show()
print('Accuracy of fitted parameters')
plot_parameter_accuracy(sim_epoch_fit_4)
Distribution of input parameters
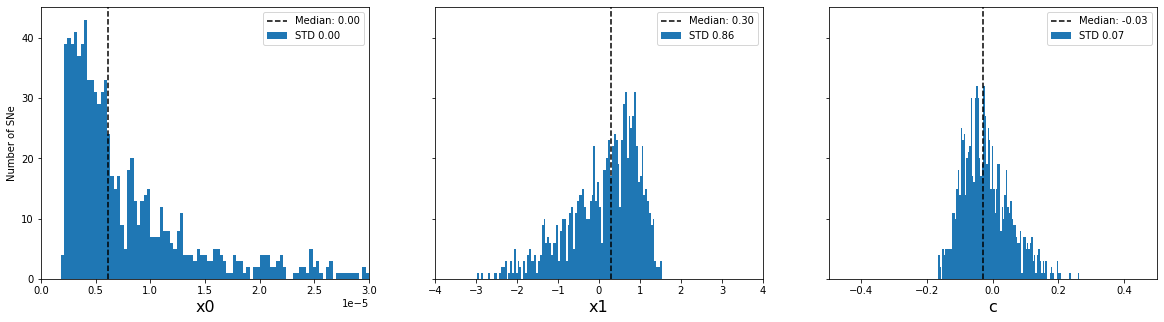
Accuracy of fitted parameters
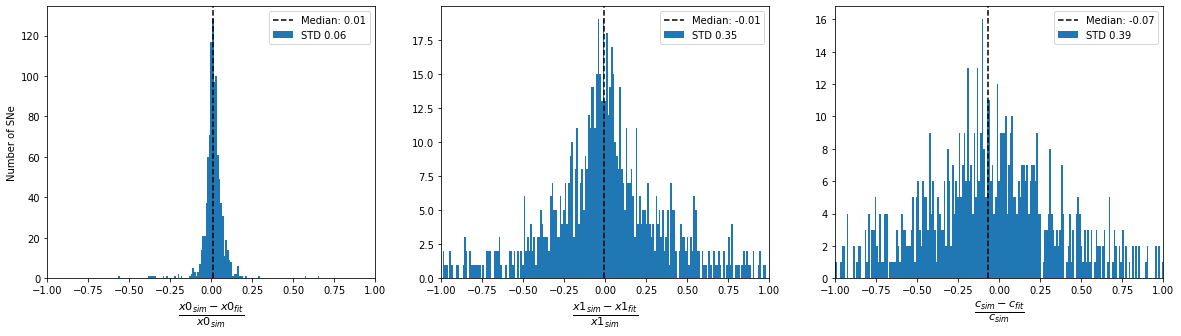
[13]:
print('Distribution of input parameters')
plot_parameter_distribution(sim_epoch_fit_seasonal)
plt.show()
print('Accuracy of fitted parameters')
plot_parameter_accuracy(sim_epoch_fit_seasonal)
Distribution of input parameters
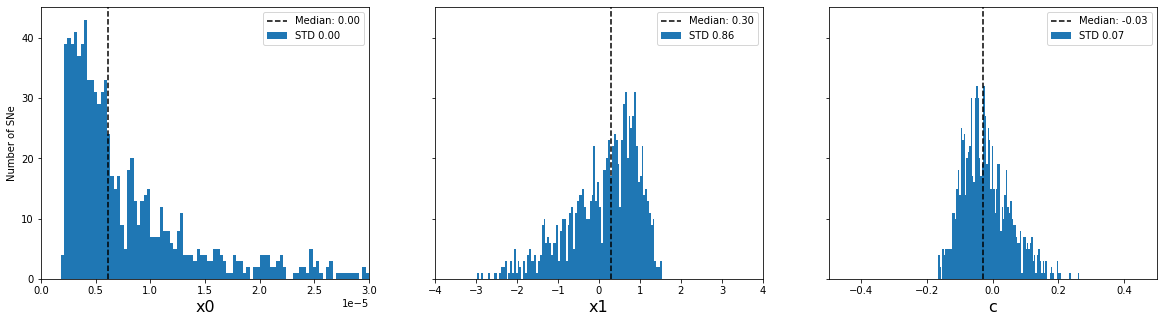
Accuracy of fitted parameters
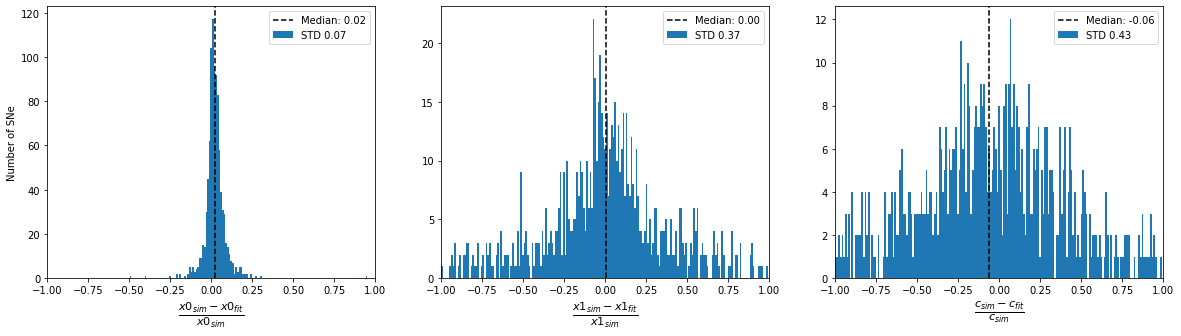
[14]:
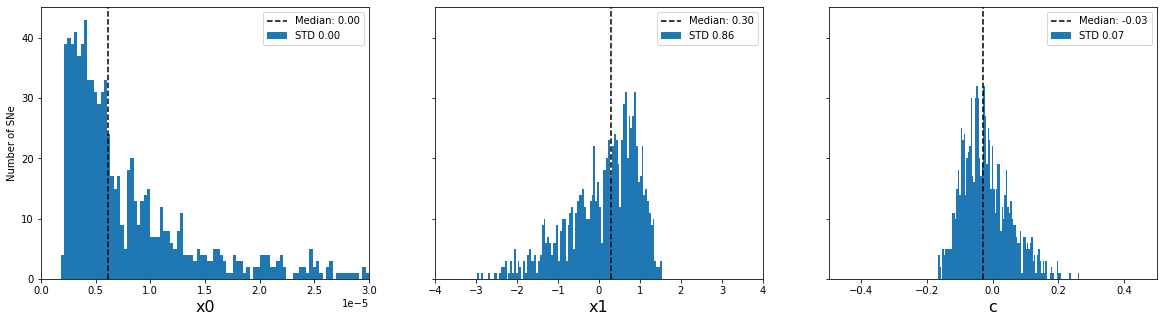
print('Distribution of input parameters')
plot_parameter_distribution(sim_epoch_fit_epoch)
plt.show()
print('Accuracy of fitted parameters')
plot_parameter_accuracy(sim_epoch_fit_epoch)
Distribution of input parameters
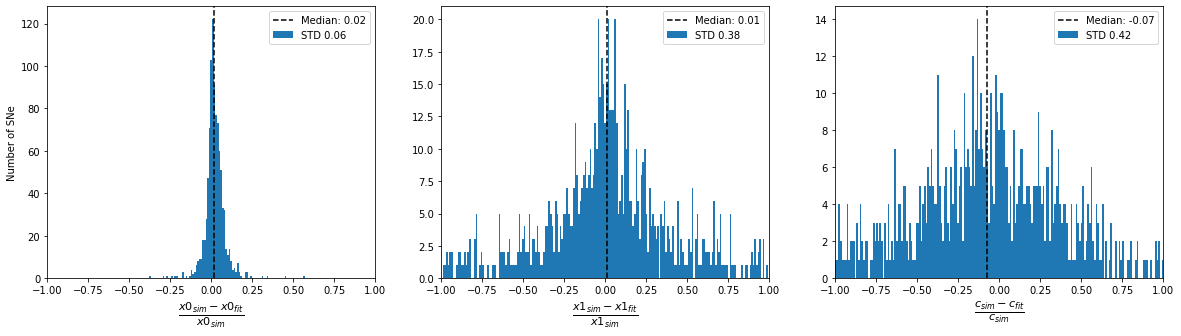
Accuracy of fitted parameters
Correlation Between Residuals and SN Properties¶
We check for correlations between residuals in the fitted parameters and other supernova properties.
[15]:
def calc_correlations(
data,
params=('delta_t0', 'delta_x0', 'delta_x1', 'delta_c'),
properties=('z', 't0', 'x0', 'x1', 'c', 'ra', 'dec'),
):
"""Calculate the pearson correlation coefficiant between the
accuracy in fitted parameters and SN properties
Args:
data (DataFrame): Pipeline data to use for the plot
params (tuple): Model parameters to calculate covariance for
properties (tuple): Name of SN properties to calculate covariance with
Returns:
- A dataframe with covariance values
- A dataframe with p values
"""
data = clean_data(data)
corr_for_param = dict()
p_for_param = dict()
for param in params:
corr_for_prop = dict()
p_for_prop = dict()
for prop in properties:
x = data[prop]
y = data[param]
corr_for_prop[prop], p_for_prop[prop] = pearsonr(x, y)
corr_for_param[param] = pd.Series(corr_for_prop)
p_for_param[param] = pd.Series(p_for_prop)
return pd.DataFrame(corr_for_param), pd.DataFrame(p_for_param)
[16]:
def plot_correlations(
corr_data,
params=('delta_t0', 'delta_x0', 'delta_x1', 'delta_c'),
properties=('z', 't0', 'x0', 'x1', 'c', 'ra', 'dec'),
figsize=(8, 8),
vmin=None,
vmax=None,
label='',
cmap=None
):
"""Create a heatmap of correlation data
Args:
corr_data (DataFrame): Data returned from ``calc_correlations``
params (tuple): Model parameters used to calculate covariance
properties (tuple): Name of SN properties used to calculate covariance
figsize (tuple): Size of the generated figure
vmin (int): Lower bound of the color bar
vmax (int): Upper bound of the color bar
label (str): The label of the color bar
cmap (str): Name of the matplotlib color map to use
"""
fig, axis = plt.subplots(figsize=figsize)
im = axis.imshow(corr_data, vmin=vmin, vmax=vmax, cmap=cmap)
cbar = axis.figure.colorbar(im, ax=axis)
cbar.ax.set_ylabel(label, rotation=-90, va="bottom")
axis.set_xticks(np.arange(corr_data.shape[1]))
axis.set_yticks(np.arange(corr_data.shape[0]))
axis.set_xticklabels(params)
axis.set_yticklabels(properties)
[17]:
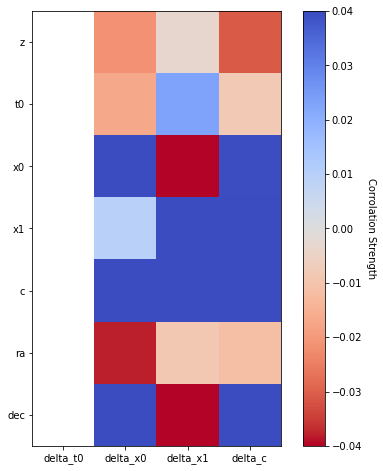
corr, p = calc_correlations(sim_epoch_fit_4)
print('Correlation matrix:')
plot_correlations(corr, vmin=-.04, vmax=0.04, label='Corrolation Strength', cmap='coolwarm_r')
print(corr)
plt.show()
Correlation matrix:
delta_t0 delta_x0 delta_x1 delta_c
z NaN -0.021312 -0.003353 -0.030628
t0 NaN -0.016767 0.022884 -0.008252
x0 NaN 0.399608 -0.048634 0.039499
x1 NaN 0.009479 0.047773 0.041796
c NaN 0.046033 0.049560 0.045537
ra NaN -0.038020 -0.008513 -0.011467
dec NaN 0.042037 -0.071100 0.048980
/home/djperrefort/miniconda3/envs/SN-PWV/lib/python3.9/site-packages/scipy/stats/stats.py:4023: PearsonRConstantInputWarning: An input array is constant; the correlation coefficient is not defined.
warnings.warn(PearsonRConstantInputWarning())
[18]:
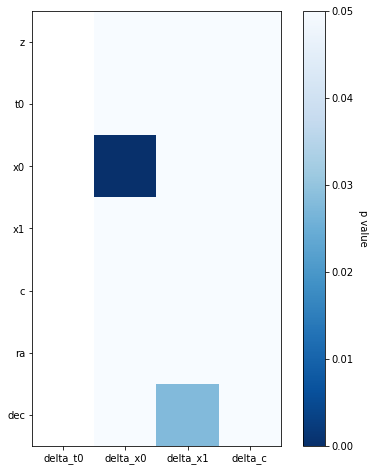
print('p-value matrix:')
plot_correlations(p, label='p value', cmap='Blues_r', vmax=0.05)
print(p)
plt.show()
p-value matrix:
delta_t0 delta_x0 delta_x1 delta_c
z NaN 5.102102e-01 0.917497 0.343910
t0 NaN 6.044322e-01 0.479501 0.798767
x0 NaN 5.351855e-38 0.132725 0.222159
x1 NaN 7.696231e-01 0.139731 0.196408
c NaN 1.547531e-01 0.125501 0.159255
ra NaN 2.399768e-01 0.792529 0.723115
dec NaN 1.938372e-01 0.027847 0.129987
[19]:
def density_plot(
data,
y_vals=('x0', 'x1', 'c'),
y_lims=((-1, 1),) * 3,
y_bins=200,
x_vals=('x0', 'x1', 'c'),
x_lims=((0, 3.0e-05), (-5, 5), (-0.25, 0.25)),
x_bins=200,
color_bins=50,
cmap='Blues',
figsize=(20, 20)
):
"""Plot 2d histogram of the normalized difference between
simulated and fitted model parameters relative to a given
dataframe column.
Args:
data (DataFrame): Pipeline data to use for the plot
params (tuple): Tuple of parameter names to plot distributions for
x_val (str): Name of column to use for the x axis
figsize (tuple): Size of the generated figure
bins (int): Number of bins to use in the histogram
cmap (str): Name of the color map to use
"""
num_xvals = len(x_vals)
num_yvals = len(y_vals)
num_columns = num_xvals + 1
num_rows = len(y_vals) + 1
fig = plt.figure(figsize=figsize)
gs = fig.add_gridspec(
num_rows,
num_columns,
width_ratios=(6,) * num_xvals + (3,),
height_ratios=(3,) + (6,) * num_yvals,
# left=0.1,
# right=0.9,
# bottom=0.1,
# top=0.9,
# wspace=0.05,
# hspace=0.1
)
# Iterate over center subplots and add 2d histograms
for row_idx, (y_val, y_lim) in enumerate(zip(y_vals, y_lims), start=1):
for col_idx, (x_val, x_lim) in enumerate(zip(x_vals, x_lims)):
# Drop nans
plt_data = data.dropna(subset=[x_val, f'delta_{y_val}_norm'])
x_data = plt_data[x_val]
y_data = plt_data[f'delta_{y_val}_norm']
ax = fig.add_subplot(gs[row_idx, col_idx])
ax.hist2d(x_data, y_data, bins=color_bins, cmap=cmap, range=(x_lim, y_lim))
ax.set_xlim(x_lim)
ax.set_ylim(y_lim)
if col_idx == 0:
ax.set_ylabel(r'$\frac{' + y_val + r'_{sim} - ' + y_val + '_{fit}}{' + y_val + '_{sim}}$', fontsize=16)
if row_idx == num_yvals:
ax.set_xlabel(x_val, fontsize=16)
# Iterate over top most row and add histograms
for col_idx, (x_val, x_lim) in enumerate(zip(x_vals, x_lims)):
top_of_column_ax = fig.add_subplot(gs[0, col_idx])
top_of_column_ax.hist(data[x_val], bins=np.linspace(*x_lim, x_bins))
top_of_column_ax.set_xlim(x_lim)
# Iterate over right most column and add histograms
for row_idx, (y_val, y_lim) in enumerate(zip(y_vals, y_lims), start=1):
end_of_row_ax = fig.add_subplot(gs[row_idx, num_xvals])
end_of_row_ax.hist(data[f'delta_{y_val}_norm'], bins=np.linspace(*y_lim, y_bins), orientation='horizontal')
end_of_row_ax.set_ylim(y_lim)
[20]:
density_plot(sim_epoch_fit_4)
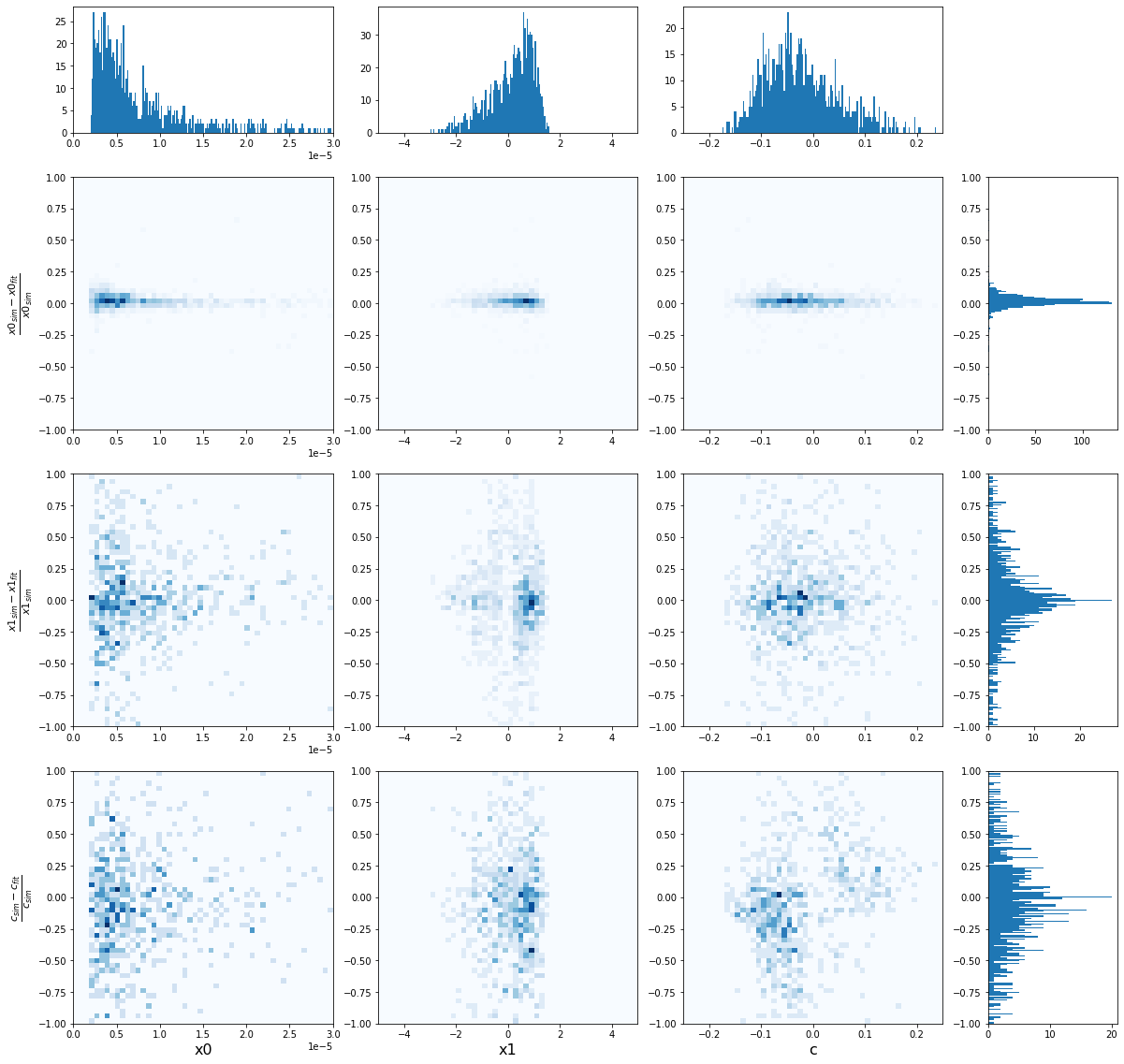
[21]:
def plot_ra_dec(data, param, cmap='bwr'):
"""Plot normalized residuals on a sky map
Args:
data (DataFrame): Pipeline data to use for the plot
param (str): Name of the parameter to plot accuracy for
cmap (str): Name of the color map to use
"""
resid = data[f'delta_{param}_norm']
median_resid = resid.median()
sn_coord = SkyCoord(data['ra'], data['dec'], unit=u.deg).galactic
plt.figure(figsize=(10, 5))
plt.subplot(111, projection='aitoff')
plt.grid(True)
scat = plt.scatter(
sn_coord.l.wrap_at('180d').radian,
sn_coord.b.radian, c=resid,
vmin=-1 + median_resid,
vmax=1 + median_resid,
s=1,
cmap=cmap)
plt.colorbar(scat).set_label(f'Accuracy in {param} (Median = {median_resid:.2f})', rotation=270, labelpad=15)
[22]:
plot_ra_dec(sim_epoch_fit_4, 'x0')
/home/djperrefort/miniconda3/envs/SN-PWV/lib/python3.9/site-packages/numpy/lib/function_base.py:3615: RuntimeWarning: invalid value encountered in true_divide
return sin(y)/y
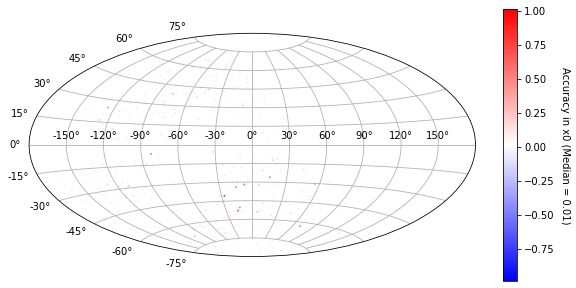
[23]:
plot_ra_dec(sim_epoch_fit_4, 'x1')
/home/djperrefort/miniconda3/envs/SN-PWV/lib/python3.9/site-packages/numpy/lib/function_base.py:3615: RuntimeWarning: invalid value encountered in true_divide
return sin(y)/y
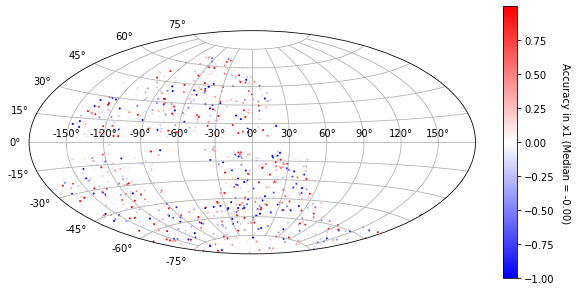
[24]:
plot_ra_dec(sim_epoch_fit_4, 'c')
/home/djperrefort/miniconda3/envs/SN-PWV/lib/python3.9/site-packages/numpy/lib/function_base.py:3615: RuntimeWarning: invalid value encountered in true_divide
return sin(y)/y
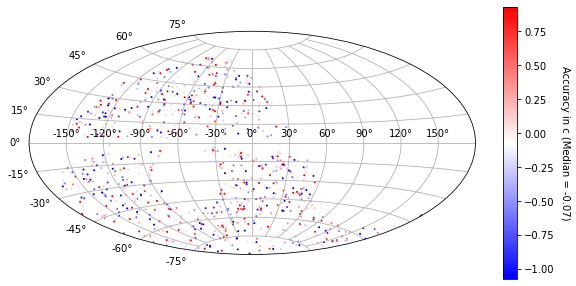
[ ]: